Understanding Grover's algorithm on cnot.io
15 May 2022
Understanding cnot.io: grover’s algorithm circuit.
I will explain much of the concepts using the simulation in this page
Prerequisites
Traits of Hadamard Gate
Hadamard gate splits the probability, and it is it’s own inverse.
As you can see in these pictures, if the input was |0> then after two hadamard gate the result goes back to |0>.
However if we switches the state of the qubit by applying Z-gate after the H-gate
and apply the H-gate again, the result goes to |1>
Traits of CNOT Gate
In CNOT gate the control qubit (first one) flips the target qubit (second one), if and only if the control qubit is |1>.
As you can see in this picture, when we put the control qubit in superposition |+> by applying H-gate the formula goes to:
CNOT|0+> = 1/(2^(1/2)) ( |00> + |11>)
Phase Kickback
If we put the target qubit in superposition as well in the circuit above, the state formula goes to:
|++> = 1/2 (|00> + |01> + |10> + |11>)
If we put the target qubit into |-> state by applying Z gate, then the state formula goes to:
|-+> = 1/2 (|00> + |01> - |10> - |11>) = = |-->
As you can see the state of the control qubit is affected, while the phase of the target qubit isn’t affected. This is called phase kickback technique.
The Quantum Oracle
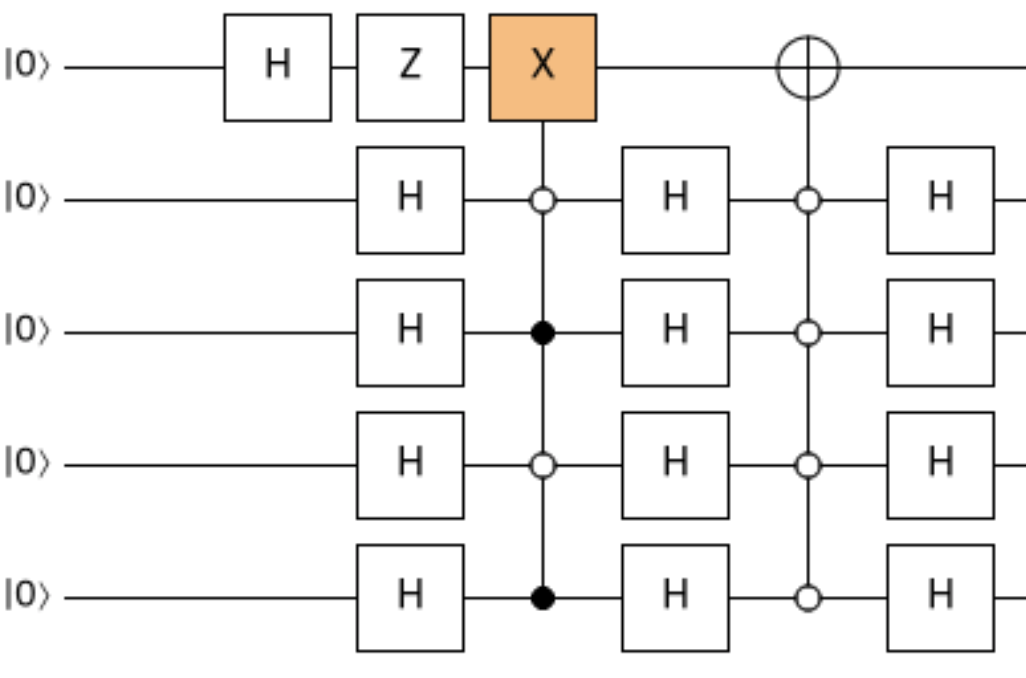First thing we need to do for the algorithm is to construct the quantum oracle circuit.
This is the quantum oracle circult proposed in the cnot.io’s post.
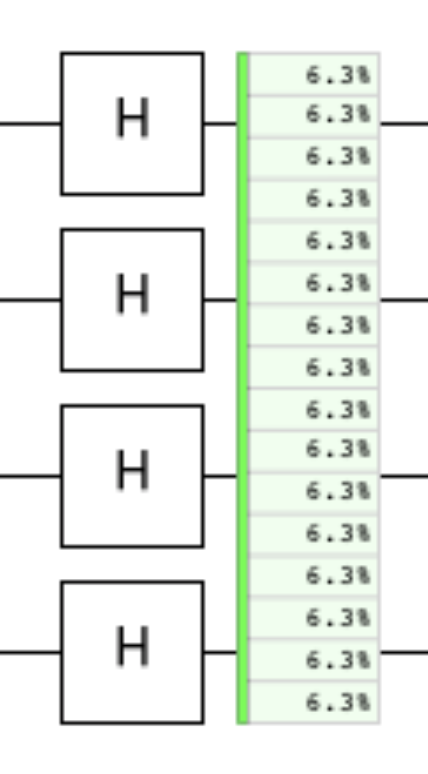As you can see, after the qubit passes each hadamard operators all possible states exist with the probability: 1/(2^4)
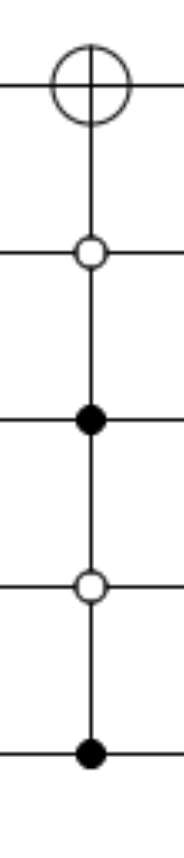
Then we setup the Toffoli gate (extended version of CNOT gate).
As the target state we searching for is |1010⟩, the cnot gates are set in this way, with two controls and two anti-controls.
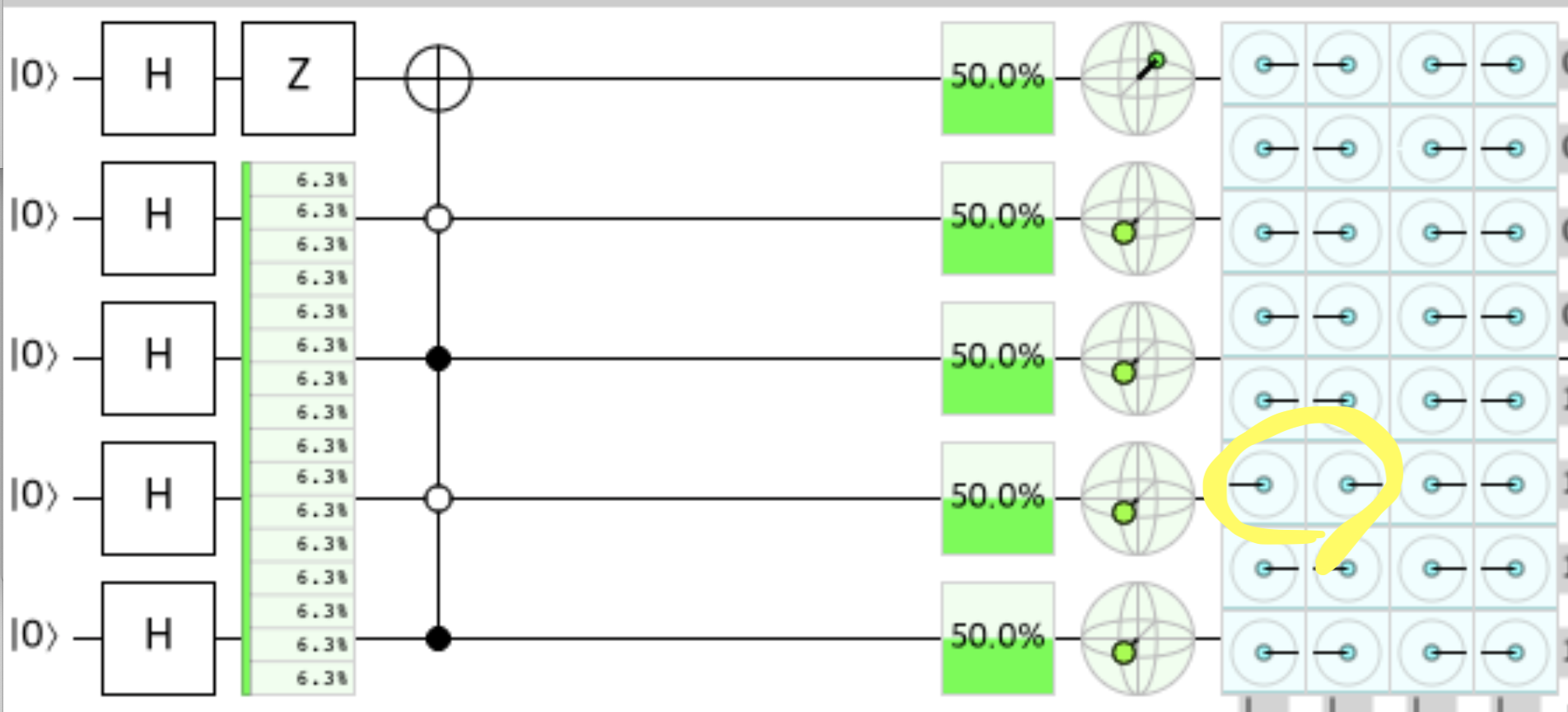
This is where the phase kickback technique shows up.
As you can see, after applying the toffoli gate and making the target qubit as |-> with applying H-gate and Z-gate the phase of the answer state |1010> has been switched.
To be more specific, the phases of the |10101> |10100>, including the target bit’s state, has been switched.
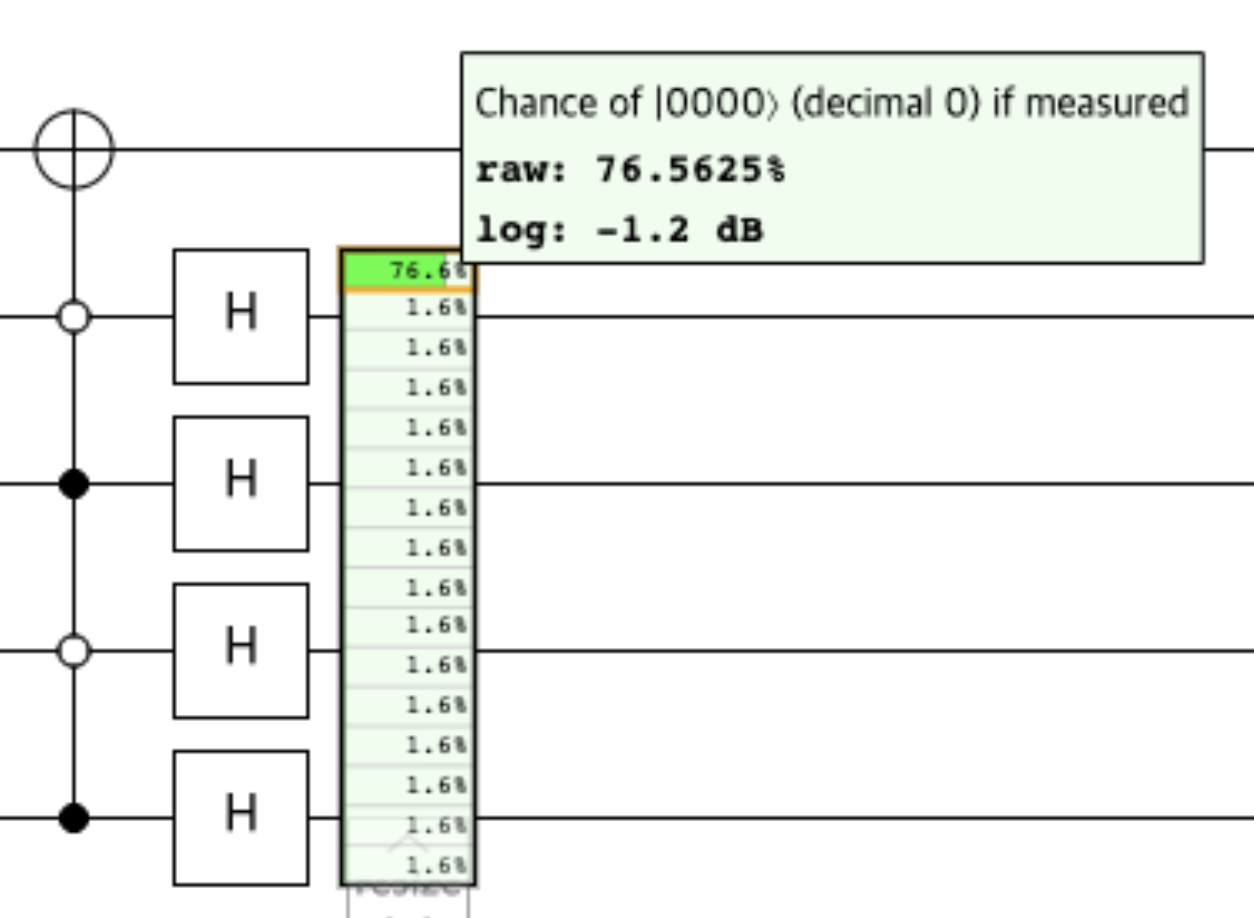
After that, all states passes H-gates again. As I mentioned above in Traits of Hadamard gate, only the states whose phase are unchanged goes back to the original state= |0000>, by applying H-gate again.
Diffusion Operator
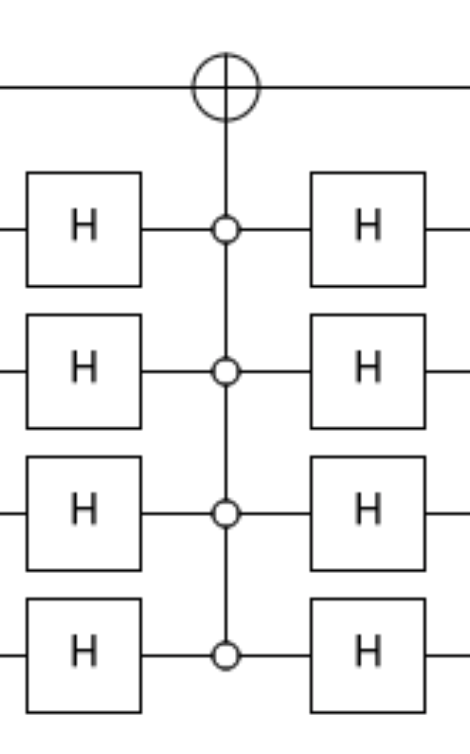Next thing to do is constructing the diffusion operator.
Once again we use the kickback technique but this time the target is |0000> which is the original state.
After passing the toffoli gate, the phase of the state |0000> is switched, and any other state’s phases stay unchanged.
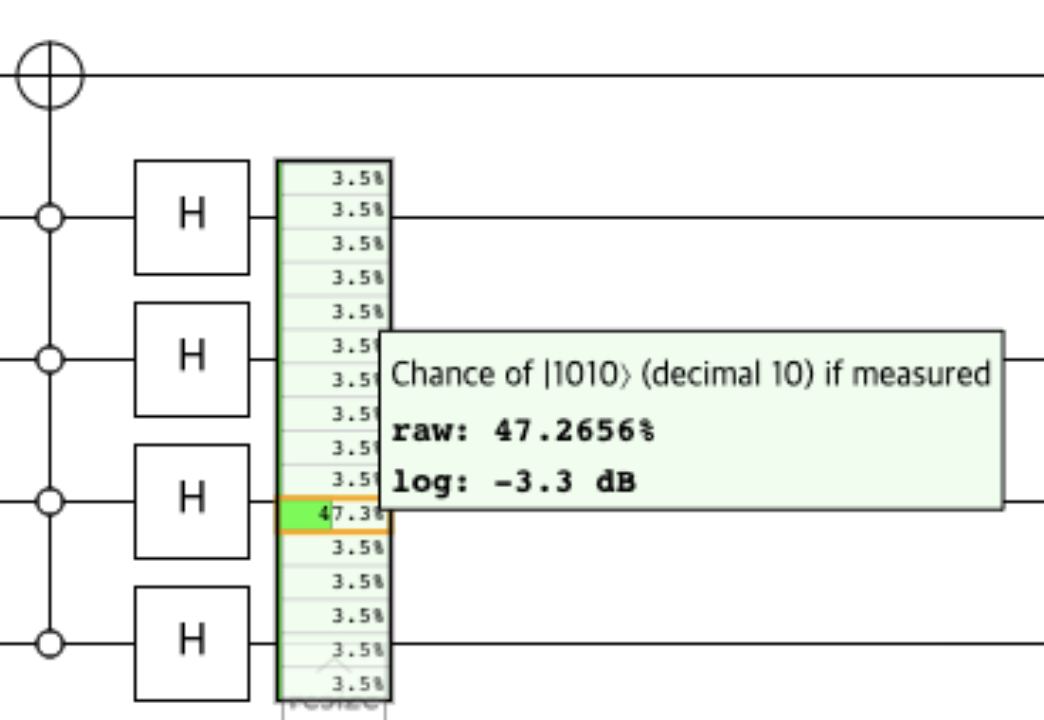Then we apply the Hadamard gates again, then we can get the answer with certain probability.
Then repeat the whole circuit (quantum oracle + diffusion operator) O(sqrt(N)) times.
Summary
This is the concepts of the circuit proposed in cnot.io: grover’s algorithm, as I understand.
However, I still cannot figure out why the probability of |0000> becomes 76.5625% = (7/8)^2 at the end of the Quantum oracle circuit,
or why the probability of getting answer becomes 47.2656% after the diffusion operator. I’ll add extra explanation about those probabilities later, if I can.
References
https://algassert.com/quirk
https://qiskit.org/textbook/ch-gates/phase-kickback.html
https://cnot.io/quantum_algorithms/grover/