Linear Model
26 May 2022
0.1. Linear, Non-Linear
Superposition Principle
The linear coupling of the solution of the linear differential equation becomes another solution of the linear differential equation.
Differential equation: an equation consisting of unknown functions and their schematics.
Linear coupling: computations in which vectors are combined with scalar multiplication and addition of vectors to obtain new vectors. ex) x[3 1]+y[−1 1]=[−2 2]
Linear Function
f(x) = ax + b
x1 + x2 = x3
When y1 = f(x1) and y2 = f(x2), y3 = f(x1 + x2) = y1 + y2
Non-Linear Function
f(x) = ax²
x1 + x2 = x3
When y1 =f(x1) and y2 = f(x2), y3 != f(x1 + x2) != y1 + y2
If a function is Linear, one function value can be easily inferred from several different function values.
0.2. Regression
Data analysis method which explains dependent variable=y with other variables x1,x2, …, xn.
Dependent variables are also called as response variables. The variables used for explanation are called explanatory variables or independent variables.
“Regression”
Regression analysis is known to have been established by biologist Francis Golton. ‘Return to Mean’ refers to the tendency of being closer to the average of previously measured data, even if extreme values were detected that could not be easily imagined when quantified and measured.
In modern times, the meaning of returning to a regress, or average, has almost disappeared. These days, most methodologies that set up independent and dependent variables and look at their relationships statistically are sometimes called regression.
0.3. Logistic
Leibniz tried to solve logical problem in a mathematical way, based on the fact “While philosophers who pursue truth always argue, mathematicians who do calculations always try to solve logical problems in a mathematical way always achieve consensus”.
…
The characteristic of all of these calculations is to apply the functional law by displaying symbols such as numbers and letters used in the calculation, and the reciprocal functions of those symbols are also marked with symbols.
…
Logical calculations are referred to as “symbolic logic” because they are represented by symbols such as p, q, p’ and q’ for example, and by symbols such as the functional relationship between two propositions,
i.e. function relationships, for example → (inserting), &(b) and v(or) and ~(negative). ..?
0.4. Bayes’ theorem
If
P(A) and P(B) independent
P(A) = Probability of A occurring
P(B) = probability of B occurring
P(B|A) = The probability that B will occur after A occurs
P(A|B) = The probability that A will occur after B occurs
then
P(A|B) = P(B|A) P(A) P(B)
0.5. maximum likelihood method
To calculate the population parameters of a probability variable based on the values collected from a probability variable.
That is, To obtain a population parameter that maximizes the likelihood that the desired values will come out when given.
When Probability variable set D = (X1,X2, …when there is, Xn) and its probability mass function f and X1, X2, …, if the Xn is independent and has the same probability distribution, then the probability L is
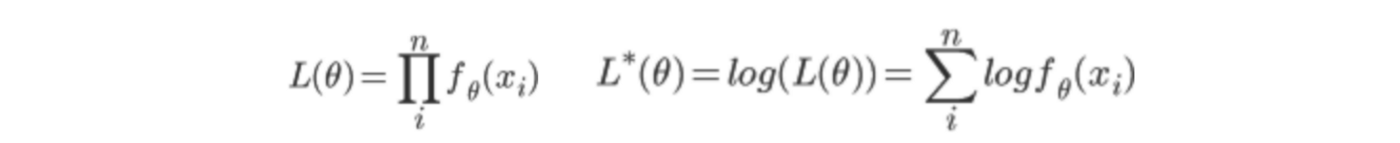
1. Linear Regression Analysis
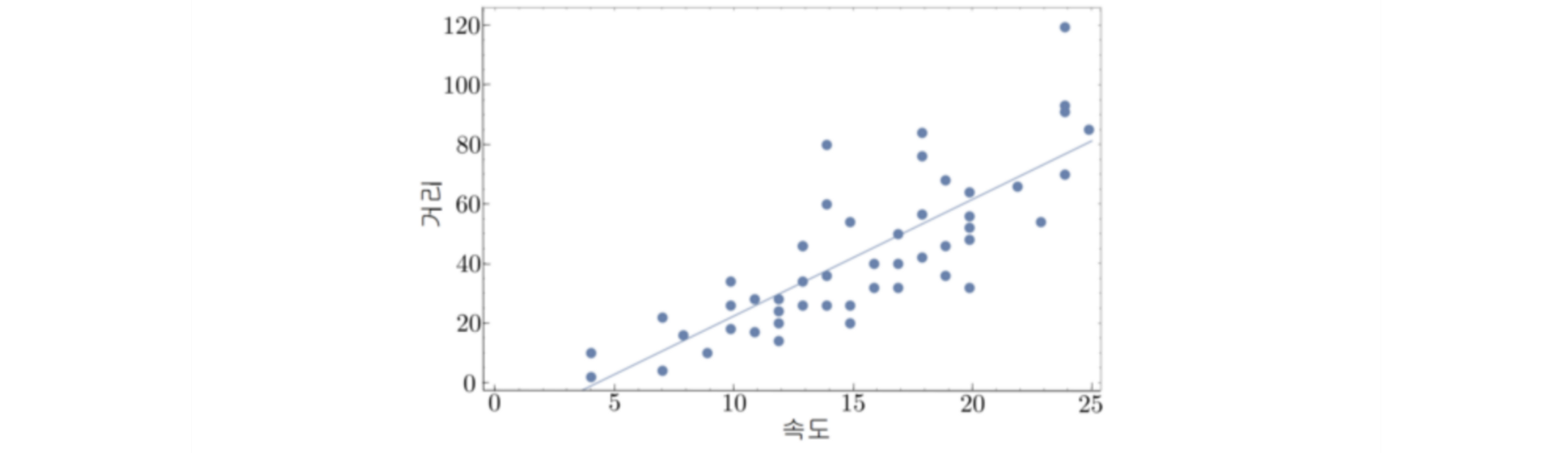
y= wTx + a + ε
where wx + a is the theoretically derived value, ε is the error term. The goal of linear regression is to minimize ε, which generally assumes that
(1) ε Follow the normal distribution. If y¡¡ can be measured many times for a particular value x¡, then it is distributed in a form close to the normal distribution.
(2) The expected value of ε is 0. If y¡¡ can be measured several times against a specific value x¡ and a large number of ε¡ measurements can be obtained, the mean will be zero.
(3) The variance of ε shall not be varied by the value of x. In other words, the accidental interaction method is not changed by the value of x.
(4) Each of the other observed values shall be independent. Accidents due to unique circumstances in one observation do not affect another.
(5) The value of x does not depend on ε, i.e. coincidence. The only thing that depends on ε is the measured value of y.
With these assumptions, our goal is to induce an error, namely the sum of the squared errors = SSE(w).
Minimizing estimation errors also maximizes the likelihood, leading to LL(w) in the SSE(w) expression.
We go through the process of solving this again in the way of w.
2. Logistic Regression
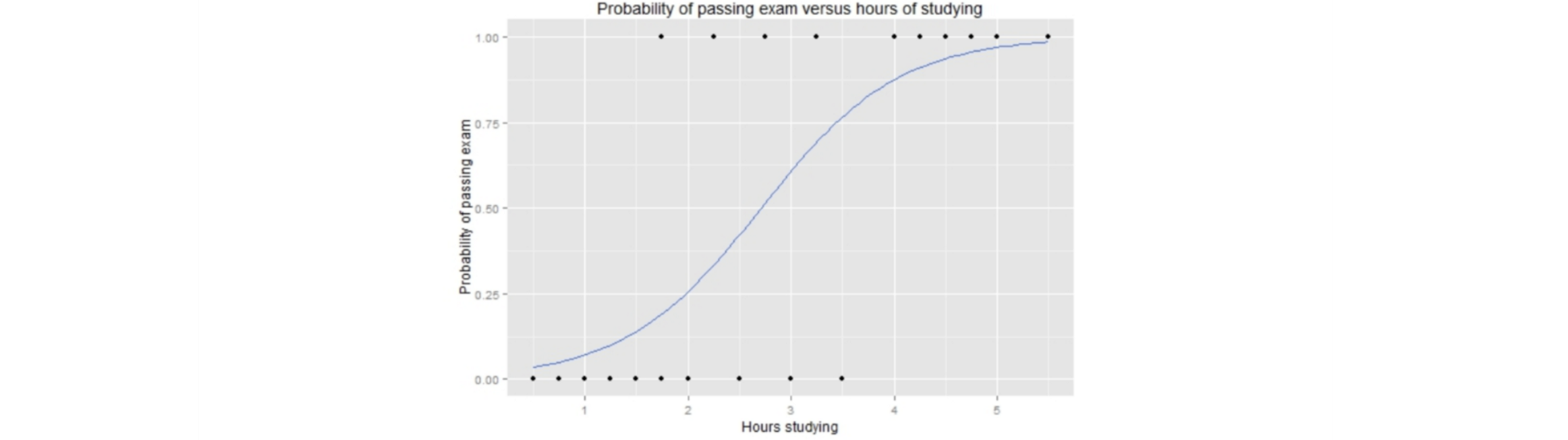
To classify results using linear combinations of independent variables
If the classification results are 0 and 1, then it is called Binary Logistic Regression, and if it is more than that, it is called Multinomical Logistic Regression.
2.1 Binary Logistic Regression
The goal in binary classification is to find a line that separates the two classes.
If the response variable y-value is Pr (y = c | x, k), then the probability that it belongs to 0 and the probability that it belongs to 1 is that
Pr( y = 0 | x), Pr( y = 1 | x)
Pr( y = 0 | x) + Pr( y = 1 | x) = 1
The slope of the line is that
Pr( y = 0 | x) / Pr( y = 1 | x) (1)
With applying log
log ( Pr(y = 0 | x) / Pr( y = 1 | x)) (2)
As the boundary line is represented by wTx In linear coupling
log ( Pr(y = 0 | x) / Pr( y = 1 | x)) = wTx (3)
WIth (1) and (3), Solving P(y = 1|x) and P(y = 0|x) goes to
Pr(y = 1|x) = 1 / (1 + exp(-wTx)) (4)
Pr(y = 0|x) = exp(-wTx) / (1 + exp(-wTx)) (5)
With calling (4) as g(wTx), {5} becomes 1 - g(wTx).
g(wTx) is used to calculate the class probability as a logistic function.
(Plus, The reason why you taking log in (2) is because, If you don’t take the log, the logistic function becomes 1 / (1-wTx).
This function is not appropriate because the closer x becomes 0, the closer the y-value becomes infinite)
Multinomial Logistic Regression
Pr( y = c | x) for class c is that
Pr( y = c | x) = exp((wc)Tx) / Sum(j)(exp((wc)Tx))
This is generalized for vector vj and is defined as softmax function:
softmax(i, v) = exp(vi) / Sum(j)(exp(vj))
4. Naive Bayes Regression
Naive Bayee is a simple technique for creating classifiers and is trained using multiple algorithms based on general principles, not through training through a single algorithm.
All Naive Bayes classifiers commonly assume that all characteristic values are independent of each other.
For example, the characteristics that enable a particular fruit to be classified as an apple (round, red, 10 cm in diameter) assume that there is no association that can occur between the characteristics in the Naive Bayes classifier and that each characteristic contributes independently to the probability that a particular fruit is an apple.
References
LinearityNonlinearityFunction
https://terms.naver.com/entry.nhn?docId=3338196&cid=47324&categoryId=47324
https://terms.naver.com/entry.nhn?docId=2365700&cid=50762&categoryId=51340
taeoh-kim maximum likelihood
https://icim.nims.re.kr/post/easyMath/64
https://wikidocs.net/22892
https://wikidocs.net/7679
https://ratsgo.github.io/machine%20learning/2017/05/18/naive/